MINI RISET
![Raja Bunglon]()
by
Raja Bunglon
Oktober 07, 2019
MINI RISET PEMODELAN Metode Lagrange Multiplier Mengantisipasi Kendala Ruang Penyimpanan dan Biaya Persedaan
MINI RISET PEMODELAN Metode Lagrange Multiplier
BAB I
PENDAHULUAN
1.1 Latar Belakang Mini Riset
Cabang Distributor Penjualan Minuman Jus buah “X” di Marihat bandar ,dalam kegiatan produksinya hanya mengelola produk jadi dalam jumlah banyak dan terdiri dari berbagai jenis produk (multi item). Produk jadi tersebut dalam kondisi siap dipasarkan, yang sebelumnya harus mendapat perlakuan penyimpanan untuk persediaan kebutuhan penjualan pada waktu selanjutnya dalam jangka waktu tertentu. Di perusahaan ini, sering terjadi kondisi overstock atau kelebihan persediaan pada produk jenis tertentu dan kondisi stockout atau kekurangan persediaan pada produk jenis tertentu pula. Hal ini terjadi karena untuk masing-masing produk dengan berbagai tipe/jenis tersebut memiliki tingkat penjualan yang berbeda-beda.
Selain itu, ruang penyimpanan Minuman Jus buah juga terbatas. Bila terjadi kelebihan persediaan pada satu atau beberapa jenis Minuman Jus buah– karena penjualan menurun – maka kapasitas ruang penyimpanan akan bertambah jika dilakukan penambahan jumlah persediaan. Sama halnya dengan nilai investasi persediaan yang akan meningkat. Metode Lagrange Multiplier digunakan untuk melakukan perencanaan persediaan produk multi item dengan kendala, yang dalam hal ini kendala-kendala tersebut adalah keterbatasan ruang penyimpanan dan nilai investasi persediaan.
I.2 Rumusan Masalah
Permasalahan yang perlu dirumuskan dalam Mini Riset ini adalah: “Bagaimana metode Lagrange Multiplier sebagai sistem perencanaan persediaan produk multi item Minuman Jus buah perusahaan X di Marihat Bandar dapat mengantisipasi kendala kapasitas ruang penyimpanan dan biaya persediaan, sehingga diperoleh jumlah pemesanan yang optimal?”
1. 3 Tujuan Mini Riset
Mini Riset ini dilakukan dengan tujuan untuk menganalisis sistem perencanaan dan pengendalian persediaan produk jadi multi-item Minuman Jus buah perusahaan X diMarihat Bandar yang optimal berdasarkan kendala kapasitas ruang penyimpanan dan biaya persediaan dengan metode Lagrange Multiplier.
1.4 Asumsi-asumsi
Asumsi-asumsi yang digunakan antara lain:
a. Mini Riset ini hanya melibatkan item produk Minuman Jus buah dari hasil penjualannya di perusahaan “X” Marihat Bandar.
b. Perhitungan biaya-biaya persediaan dalam rentang waktu mingguan dengan satu bulan ada 4 (empat) minggu.
c. Jumlah hari kerja dalam satu bulan adalah setiap hari.
d. Jumlah biaya yang digunakan setiap ada pemesanan dianggap tersedia.
e. Gudang penyimpanan produk dianggap dapat menampung jumlah produk yang dipesan.
f. Dalam Mini Riset ini tidak akan membahas struktur organisasi perusahaan dan aspek finansialnya, walaupun ada keterkaitan dengan persediaan. Jadi, Mini Riset ini hanya dibatasi pada data-data harga produk, biaya penyimpanan, biaya pemesanan, dan batasan ruang gudang penyimpanan.
BAB II
TINJAUAN PUSTAKA
2.1 Persediaan
Persediaan (inventory) merupakan stok barang yang disimpan oleh suatu perusahaan untuk memenuhi permintaan pelanggan.Umumnya setiap jenis perusahaan memiliki berbagai bentuk persediaan. Berdasarkan jenis dan posisi barang dalam urutan pengerjaan produk, persediaan dapat dibagi menjadi lima macam, yaitu [5]:
1 Persediaan bahan baku, yaitu persediaan dari barang-barang berwujud yang digunakan dalam proses produksi.
2 Persediaan komponen produk atau parts yang dibeli, yaitu persediaan barang-barang yang terdiri dari parts yang diterima dari perusahaan lain, yang dapat secara langsung di-assembling dengan parts lain tanpa melalui proses produksi sebelumnya
3 Persediaan bahan-bahan pembantu atau barang-barang perlengkapan, yaitu persediaan barang-barang atau bahan baku yang diperlukan dalam proses produksi untuk membantu kelancaran produksi.
4 Persediaan barang setengah jadi, yaitu persediaan barang-barang yang keluar dari tiap-tiap bagian dalam suatu pabrik atau barang yang masih perlu diproses kembali untuk kemudian menjadi barang jadi.
5 Persediaan barang jadi, yaitu persediaan barang-barang yang telah selesai diproses atau diolah dalam pabrik dan siap untuk dijual kepada para konsumen atau perusahaan lain.
2.2 Biaya-Biaya Persediaan
Biaya-biaya persediaan ini timbul karena adanya rencana persediaan dalam perusahaan untuk memperlancar kegiatan produksi.Biaya-biaya akibat pengelolaan persediaan dibedakan menjadi enam, yaitu [3]:
a. Cost item atau harga barang per unit, yaitu biaya yang timbul karena adanya harga per unit pembelian barang.
b. Ordering cost atau biaya pemesanan, yaitu biaya yang dikeluarkan berkenaan dengan adanya pemesanan barang atau bahan. Yang termasuk dalam bentuk biaya ini meliputi biaya admisnistrasi, biaya pengiriman/pengangkutan dan bongkar muat pesanan, biaya penempatan order, dan biaya pemeriksaan.
c. Holding cost atau biaya penyimpanan, yaitu biaya yang dikeluarkan berkenaan dengan adanya kegiatan penyimpanan barang/bahan yang sudah dibeli.
d. Stockout cost atau biaya kekurangan persediaan, yaitu biaya yang digunakan sehubungan dengan adanya pesediaan yang kecil dari jumlah yang dikeluarkan. Di samping itu, biaya ini timbul akibat keterlambatan pengiriman pesanan dari pemasok.
e. Biaya resiko kerusakan dan kehilangan persediaan, yaitu biaya yang timbul akibat barang persediaan telah kadaluarsa atau rusak akibat kondisi tertentu dan kehilangan persediaan.
f. Safety stock atau biaya persediaan pengaman, yaitu biaya yang dikeluarkan sehubungan dengan adanya persediaan pengaman yang berfungsi sebagai persediaan tambahan untuk melindungi dan menjaga kemungkinan terjadinya kekurangan persediaan atau biaya yang dikeluarkan sehubungan dengan adanya pesanan permintaan yang datang terlalu awal.
2.3 Model-Model Persediaan
Secara umum model persediaan dapat dikelompokkan menjadi dua bagian [4]:
a. Model Deterministik, yaitu model yang menganggap bahwa semua parameter telah diketahui dengan pasti. Model ini dibagi lagi menjadi dua yaitu deterministic static dan deterministic dynamic. Contoh model yang dipakai adalah model Economic Order Quantity (EOQ) dan pemesanan barang multi-item dengan Metode Lagrange Multiplier.
b. Model Stokastik (Probabilistik), yaitu model yang menganggap bahwa semua parameter mempunyai nilai-nilai yang tidak pasti dan satu atau lebih parameter tersebut merupakan variabel-variabel acak. Contoh dari model ini antara lain adalah model pengendalian persediaan Sistem P dan Sistem Q. Model ini dibagi lagi menjadi dua yaitu probabilistic static dan probabilistic dynamic.
2.3.1 Model Persediaan EOQ, Deterministik
Model EOQ merupakan model persediaan yang sederhana yang bertujuan untuk menentukan ukuran pemesanan yang ekonomis dan dapat meminimumkan biaya total persediaan. Model ini dapat diterapkan apabila terdapat asumsi-asumsi berikut [2]:
a. kebutuhan permintaan adalah tetap dan diketahui
b. lead time (waktu tunggu) adalah tetap
c. harga beli per unit tetap
d. biaya simpan dan biaya setiap kali pesan tetap
e. diskon kuantitas tidak diperkenankan
f. tidak terjadi kekurangan persediaan atau back order
Model ini dapat digambarkan sebagai berikut:
Qmak |
Q/2 |
O |
Waktu Pemesanan |
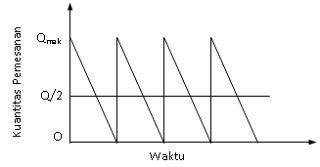
Gambar 1: Grafik Siklus Persediaan Sederhana
Dalam kaitannya dengan model persediaan tersebut, biaya-biaya yang relevan dengan model ini adalah biaya pemesanan dan biaya penyimpanan. Jika D adalah jumlah permintaan, dalam kasus ini per minggu, Q adalah kuantitas pesanan, dan S adalah biaya setiap kali pesan, maka biaya pemesanan per minggu dirumuskan:
Biaya pemesanan per minggu
Biaya simpan mingguan dihitung dengan mencari rata-rata biaya penyimpanan tiap bulan yang dikonversi menjadi mingguan. Rata-rata persediaan dihitung sebanyak setengah kali kuantitas pesanan dikali biaya simpan per unit dan nilai ini akan berkurang terus-menerus hingga mencapai nol, sehingga biaya simpan dapat dirumuskan:
Biaya penyimpanan
Berdasarkan persamaan (2.1) dan persamaan (2.2) maka biaya yang muncul dalam persediaan adalah hasil penjumlahan biaya pemesanan dan biaya penyimpanan per periode waktu, dalam kasus ini adalah per minggu, dan dapat dirumuskan sebagai:
Biaya persediaan per minggu (TC)
Hubungan dari ketiga persamaan tersebut dapat dilihat dalam Gambar 2.
Gambar 2: Kurva Biaya Persediaan
Dari Gambar 2 dapat diilustrasikan bahwa total biaya persediaan akan mencapai nilai minimum pada saat biaya simpan dan biaya pesan mencapai titik yang sama, sehingga titik minimal kurva biaya total dapat dicari dengan turunan TC terhadap Q sama dengan 0, yaitu:
Sehingga diperoleh
Q2 =
Q =
keterangan:
D = jumlah permintaan per periode (unit)
H = IP, biaya simpan per periode (Rp/unit/periode)
S = biaya pemesanan per periode (Rp/pesan)
Q = kuantitas pesanan yang optimal (unit)
P = harga satuan unit (Rp/unit)
I = biaya simpan dalam persentase persediaan (%)
2.3.2 Sistem Persediaan Produk Multi Item dengan Kendala
Banyak model persediaan yang digunakan untuk mengelola persediaan lebih dari satu tipe produk (multi item), karena umumnya banyak perusahaan yang hanya memiliki satu tempat penyimpanan namun sering digunakan untuk menyimpan lebih dari satu tipe produk. Pembahasan dalam Mini Riset ini mengacu kepada persediaan multi item produk jadi (finishedgood).
Permasalahan ini diformulasikan melalui model optimasi dengan pembatas dan penyelesaiannya menggunakan metode Lagrange Multiplier.Dalam penerapannya metode ini hanya mengacu kepada satu atau dua kendala.Kasus ini pendekatan awalnya akan mempertimbangkan permasalahan anggaran biaya dengan menghendaki pada banyak titik solusi, namun total investasi dalam persediaan tidak melebihi B satuan uang yang diwakili oleh formulasi:
dengan
Ci = harga satuan unit item produk i dalam rupiah
Qi = kuantitas pesanan optimal item produk i dalam unit
B = besarnya investasi dalam persediaan dalam rupiah
Jika n adalah jumlah item, maka tujuan dari penyelesaian permasalahan ini adalah untuk meminimisasi total biaya persediaan per periode. Sebagai langkah awal maka perlu dicari kuantitas pemesanan paling optimal dengan mengabaikan adanya konstrain atau kendala, sehingga untuk mendapatkan nilai Qi* digunakan formulasi:
Qi* =
Dari perhitungan melalui persamaan (2.11), cek kondisinya dengan mensubstitusikan nilai Qi* pada persamaan (2.10). Apabila nilai Qi* belum memuaskan, maka metode Lagrange mulai digunakan. Permasalahan ini dapat diselesaikan dengan mengembangkan Lagrange Expression (LE) atau persamaan Lagrange, yakni:
LE(Qi,l) =
Notasil adalah faktor pengali Lagrange. Dengan mengambil turunan atau derivatif dari persamaan (2.12) yang dikondisikan pada nilai Qi, l, dan menyelesaikan persamaan tersebut dengan ruas kanan disamadengankan nol, maka diperoleh formulasi:
nilai Q*Li adalah kuantitas pemesanan optimal yang diperoleh dari penggunaan metode Lagrange. Harga dari l* dapat diperoleh dengan formulasi:
l* =
kemudian mensubstitusikannya ke persamaan (2.13) dan akan memberikan persamaan:
Untuk Q*i dicari dengan persamaan (2.11) dan E dicari dengan persamaan:
E =
sedangkan untuk kendala ruang penyimpanan, total ruang penyimpanan dihitung dengan formulasi:
Selanjutnya, untuk mencari total investasi dari perhitungan Lagrange dikondisikan pada total investasi dari kebijakan perusahaan dan dapat dicari dengan formulasi:
keterangan:
Ci = harga item per unit dalam rupiah
Ai = biaya pengadaan atau pemesanan per item dalam rupiah
Di = permintaan hasil peramalan dalam unit
B = investasi maksimum yang diijinkan di perusahaan dalam rupiah
E = total investasi persediaan tanpa konstrain dalam rupiah
Q*i = kuantitas pemesanan optimal tanpa konstrain dalam unit
Q*Li = kuantitas pemesanan optimal dengan Lagrange dalam unit
Qi = kuantitas pemesanan hasil peramalan dalam unit
l* = faktor pengali Lagrange
a = biaya penyimpanan inventori dalam persentase
S = kapasitas gudang
Sa = kapasitas persediaan akhir
BAB III
PEMBAHASAN
3.1 Data
Jenis Minuman Jus buah yang dikelola untuk dipasarkan kembali oleh cabang distributor X terdiri dari 13 jenis yaitu Minuman Jus buah jeruk, Minuman Jus buah apel, Minuman Jus buah al-pukat, Minuman Jus buah jambu, Minuman Jus buah mangga, Minuman Jus buah kuini , Minuman Jus buah markisa, Minuman Jus buah sirsak, Minuman Jus buah melon, Minuman Jus buah nenas, Minuman Jus buah timun, Minuman Jus buah terong belanda, Minuman Jus buah strowbery. Ruang penyimpanan Minuman Jus buah terdiri dari tiga tempat penyimpanan dengan total kapasitas penyimpanan 150 liter.
Data penjualan Jus buah adalah sekumpulan data penjualan jus di perusahaan X dengan jangka waktu mingguan yang dihitung mulai bulan Januari 2017 sampai dengan bulan Desember 2017, yang diperoleh dari bagian pemasaran.Persentase biaya simpan diperoleh melalui persamaan [1]:
Biaya simpan/unit/minggu =
keterangan:
a = persentase biaya simpan
Pi = harga item ke-i
Qi = kuantitas item ke-i
Dengan jumlah biaya simpan sebesar Rp 175.000,- dan nilai persediaan Rp 5.700.302,08 diperoleh persentase biaya simpan per minggu tiap item yaitu sebesar 2,96 persen.
3.2 Analisis
Tabel 1 merupakan hasil perhitungan peramalan permintaan berdasarkan data historis penjualan periode Januari sampai dengan Desember 2017, dengan Mean Absolut Deviation (MAD) terkecil sebagai kriteria pemilihan metode peramalan terbaik.
Tabel 1:Hasil Peramalan dengan Kriteria MAD Terkecil untuk Minggu
Pertama Bulan Januari 2018
Jenis Produk | Hasil Peramalan Penjualan | Jenis Produk | Hasil Peramalan Penjualan |
Jus jeruk | 539,4116 | Jus nenas | 189,0000 |
Jus pokat | 122,5860 | Jus mangga | 73,9174 |
Jus markisa | 149,4992 | Jus kuini | 99,8855 |
Jus apel | 106,9206 | Jus timun | 100,3283 |
Jus sirsak | 147,6187 | Jus terong belanda | 73,3986 |
Jus jammbu | 98,9104 | Jus strowbery | 71,9128 |
Jus melon | 195,0000 |
Pengendalian persediaan ini akan menentukan tingkat persediaan yang seharusnya dilakukan dengan mempertimbangkan jumlah dan jenis jus serta kapasitas ruang penyimpanan (kulkas), sehingga jumlah jus untuk tiap item nantinya tidak akan selalu sama karena pertimbangan kendala kapasitas ruang penyimpanan dan biaya persediaan.
Sebelum dilakukan penyelesaian masalah persediaan ini dengan metode Lagrange dengan kendala, maka akan dilakukan penyelesaian tanpa kendala. Setelah diketahui nilai EOQ masing-masing item produk, maka nilai EOQ tersebut disubstitusikan ke dalam konstrain. Jika hasil perhitungan memuaskan, maka tidak perlu diselesaikan dengan metode Lagrange multi item. Namun, jika hasil perhitungan tidak memuaskan, maka dilakukan penyelesaian melalui metode Lagrange multi item.
Tabel 2:Hasil Perhitungan EOQ/Q*
Jenis Produk | Hasil EOQ/Q* (unit) | Jenis Produk | Hasil EOQ/Q* (unit) |
Jus jeruk | 344 | Jus nenas | 161 |
Jus pokat | 134 | Jus mangga | 90 |
Jus markisa | 156 | Jus kuini | 112 |
Jus apel | 88 | Jus timun | 105 |
Jus sirsak | 136 | Jus terong belanda | 60 |
Jus jammbu | 120 | Jus strowbery | 73 |
Jus melon | 185 |
Dari perhitungan Q* dengan menggunakan metode EOQ tersebut, kemudian dihitung total nilai persediaan yang baru. Dari perhitungan diperoleh nilai persediaan baru sebesar (E) Rp 6.003.493,00 dan nilai investasi persediaan ini lebih besar dari nilai persediaan lama (B) Rp 5.700.302,08. Hal ini menunjukkan kondisi belum memuaskan, maka penyelesaiannya dilanjutkan ke metode Lagrange.
Tabel 3: Hasil Perhitungan EOQ dengan Metode Lagrange/QLi*
Jenis Produk | Hasil EOQ/ QLi* (unit) | Jenis Produk | Hasil EOQ/ QLi* (unit) |
Jus jeruk | 327 | Jus nenas | 153 |
Jus pokat | 127 | Jus mangga | 86 |
Jus markisa | 148 | Jus kuini | 106 |
Jus apel | 84 | Jus timun | 100 |
Jus sirsak | 129 | Jus terong belanda | 57 |
Jus jammbu | 114 | Jus strowbery | 69 |
Jus melon | 176 |
Dari perhitungan tersebut dihasilkan kuantitas Q*Lagrange yang selanjutnya akan digunakan untuk mencari nilai total investasi persediaan yang baru dengan metode Lagrange. Dari perhitungan, diperoleh nilai investasi persediaan baru (ELagrange) sebesar Rp 5.700.302,00sehingga terjadi kondisi nilai ELagrange sama dengan nilai investasi persediaan awal (B) sebesar Rp 5.700.302,08. Ini menunjukkan bahwa perhitungan dengan konstrain biaya memberikan hasil yang memuaskan, namun untuk memastikan keakuratan metode ini perlu dilakukan perhitungan konstrain ruang.
Analog dengan perhitungan nilai investasi persediaan diperoleh kapasitas ruang terpakai sebesar 92.819 ml atau 92,819 liter, sedangkan kapasitas ruang terpakai yang tersedia di gudang sebesar 110,635 liter, sehingga kuantitas produk yang dihitung menggunakan metode Lagrange masih bisa ditampung di tempat penyimpanan atau kulkas yang tersedia. Total biaya persediaan dengan metode Lagrange sebesar Rp 140.743,00.Dengan demikian, penghematan yang diperoleh dengan metode Lagrange untuk total biaya persediaan sebesar 19,58%.
3.3 SIMPULAN
Dari hasil pengolahan dan analisis data, maka dapat ditarik simpulan bahwa dari perhitungan dengan metode Lagrange dihasilkan jumlah pemesanan optimal produk es krim Campina untuk periode minggu pertama bulan Januari 2012 adalah:
Jenis Produk | Nilai Q Lagrange | Jenis Produk | Nilai Q Lagrange |
Jus jeruk | 327 | Jus nenas | 153 |
Jus pokat | 127 | Jus mangga | 86 |
Jus markisa | 148 | Jus kuini | 106 |
Jus apel | 84 | Jus timun | 100 |
Jus sirsak | 129 | Jus terong belanda | 57 |
Jus jammbu | 114 | Jus strowbery | 69 |
Jus melon | 176 |
Hasil perolehan ini dapat memenuhi kendala ruang penyimpanan, karena total pemesanan memberikan nilai 92, 819 liter yang tidak melebihi kapasitas ruang yang masih tersisa yaitu 110, 635 liter. Selain itu, dengan sistem persediaan dengan metode Lagrange juga menghasilkan penghematan total ongkos persediaan pada minggu pertama bulan Januari 2012 sebesar 19,58%, yaitu dari Rp 175.000,00 menjadi Rp 140.743,00.
Dengan demikian, metode Lagrange lebih efektif dan efisien jika diterapkan dalam sistem pengendalian persediaan produk jadi yang bermacam-macam jenis dengan memperhatikan kapasitas ruang penyimpanan dan investasi nilai persediaan.
DAFTAR PUSTAKA
[1] Dervitsiotis, K.N. 1984. Operations Management: International Student Edition. 2nd Printing. McGraw-Hill International Book Company. Singapore
[2] Render dan Heizer. 2001. Prinsip-prinsip Manajemen Operasi. Edisi 8. Penerbit Salemba Empat. Jakarta
[3] Sumayang, L. 2003. Dasar-dasar Manajemen Produksi & Operasi. Penerbit Salemba Empat. Jakarta
[4] Taha, H.A. 1997. Riset Operasi. Alih bahasa: Daniel Wirajaya. Binarupa Aksara. Jakarta
[5] Taylor III, B.W. 2005. Sains Manajemen. Edisi 8. Penerbit Salemba Empat. Jakarta
[6] Brooks/Cole Cengange Learning 2014. A First Course In Mathematical Modeling : Frank R. Giorda, William P.Fox, Steven B. Horton.Boston, MA. USA
![KUMPULAN LIRIK [SYAIR] LAGU NIAS LAMA POPULER & TERBARU | PALING LENGKAP ~ RAJA BUNGLON](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgEw5AyLeVWxJDEXa0Zm_nl5a8TsSUBZUBNplD2-xcsnPleDeW-AlkzGQgMetDAStY79dwTIJmYZ0TvDZyaF1PHw0CqrlgkP8GIUBzFFedXCyRYmThtNwKuTsRET7cn4gZMmkI7-cuto-w/w100/QQW.png)
![KUMPULAN LIRIK [SYAIR] LAGU BATAK LAMA & TERBARU | PALING LENGKAP ~ RAJA BUNGLON](https://4.bp.blogspot.com/-O3EpVMWcoKw/WxY6-6I4--I/AAAAAAAAB2s/KzC0FqUQtkMdw7VzT6oOR_8vbZO6EJc-ACK4BGAYYCw/w100/nth.png)
Posting Komentar
0 Komentar
Mari Berdiskusi Tentang Topik Ini